Research

I am a computational and applied mathematician, and my research lies in the interdisciplinary intersection of mathematics, physics, engineering and computational science. Currently I have two main lines of research:

• Numerical analysis, and more specifically, finite element analysis, where numerical methods are developed to solve partial differential equations (PDEs) using a computer.
• Applied nonlinear dynamics, particularly hydrodynamic stability of incompressible fluid systems, where important properties are studied with the aid of a computer via semidefinite programs (SDPs) with sum-of-square (SOS) constraints.

Recently, I have tried to combine these two lines of research with the aim of resolving some logstanding problems in fluid mechanics, and this research is partially funded by the NSF.

Finite element analysis

I focus on many aspects of finite element analysis, and have developed, both in terms of software and the underlying mathematics, several finite element methods which are characterized by having:

• High-order convergence (heirarchical high-order discretizations for different element shapes and “energy” spaces).
• Proofs of numerical stability (inf-sup conditions satisfied for variational formulations).
• Adaptivity (so the meshes spatially refine in a particular area of interest).
• Desirable linear algebra properties to exploit in solvers.

Some highlights are shown next.

High-order discretizations

Unified construction of high-order hierarchical discretizations of H¹, H(curl), H(div) and L² by systematically projecting to faces and edges.

Developed a unified and systematic approach to constructing arbitrary high-order conforming discretizations of the traditional Sobolev spaces lying in a differential de Rahm sequence (H¹, H(curl), H(div) and L²) for each of the “standard” element shapes: tetrahedra,hexahedra, triangular prisms and pyramids. The code can be found here.

Discontinuous Petrov-Galerkin (DPG) methods in elasticity and viscoelasticity

Linear elasticity in the L-shape domain solved with different DPG variational formulations, all converging, but displaying different refinement patterns (left). Sheathed hose composed of a thick inner layer of rubbber, and a very thin outer layer of steel (middle). It was solved using a coupled linear elasticity DPG method which is robust in the incompressible limit inside the rubber subdomain and computationally cheap in the steel layer (right).

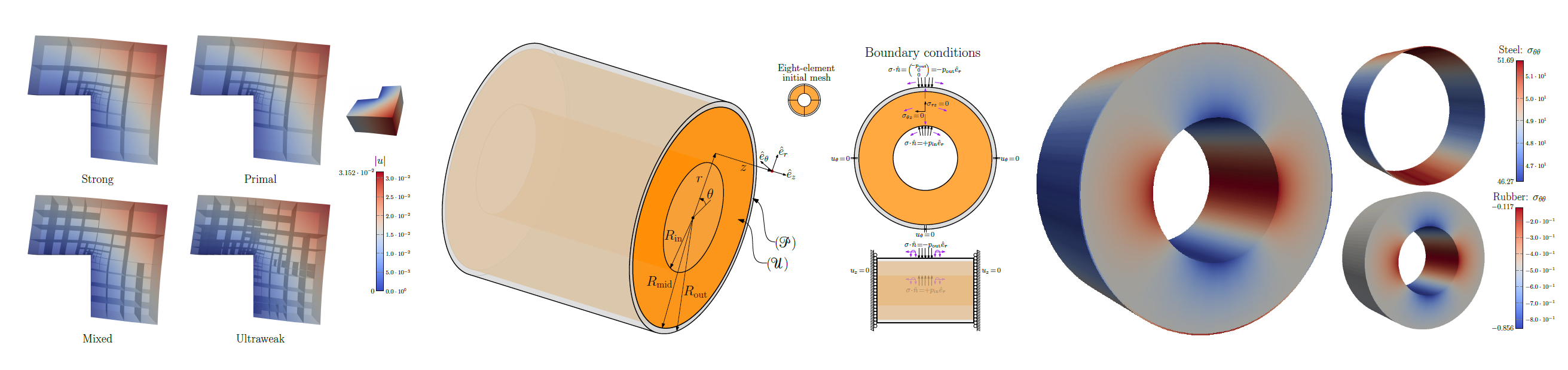
Disontinuous Petrov-Galerkin (DPG) methods are crafted to be stable for any linear well-posed variational formulation of a PDE. We showed their applicability by solving the equations of linear elasticity with various variational formulations, some being fast, others being slower, but robust in the near-incompressible limit. We also derived DPG methods that combine different formulations, as they are useful in physical problems like racing-engine hoses and biomedical devices. Using DPG methods, we also successfully validated data from dynamic mechanical analysis (DMA) calibration experiments involving viscoelastic materials to within 5% of the quantity of interest.

Experimental setup of DMA calibration experiments (left) which were then adaptively simulated using a DPG method (mid-right). By post-processing the central clamp force, the manufacturer's calibration model was validated to within 5% of experimental measurements (right).

Discrete least-squares (DLS) finite element methods

Numerically stable FEMs posed as a discrete least-squares (DLS) problem that deals directly with rectangular matrices (left). Using DLS FEMs, conditioning of near-resonant acoustics was shown to grow as O(h^-1), and the solution was found to converge even when traditional methods started to diverge (right).

As an outgrowth of DPG methods, we exploited not only that DPG methods have positive definite stiffness matrices, but that they are a product of the transpose of a known rectangular matrix times itself. Thus, it can be posed as a discrete-least squares problem and solved with much better conditioning properties via QR-based solvers. These are very suitable for ill-conditioned problems, like near-resonant acoustics.

High-order polygonal DPG (PolyDPG) methods

PolyDPG methods solve Poisson's equation using general polygonal elements including highly distorted concave elements (left), and even discontinuous material properties relevant in geophysics (middle). Polygonal refinement strategies are not limited to quadtree meshes and perform comparably with traditional methods (right).

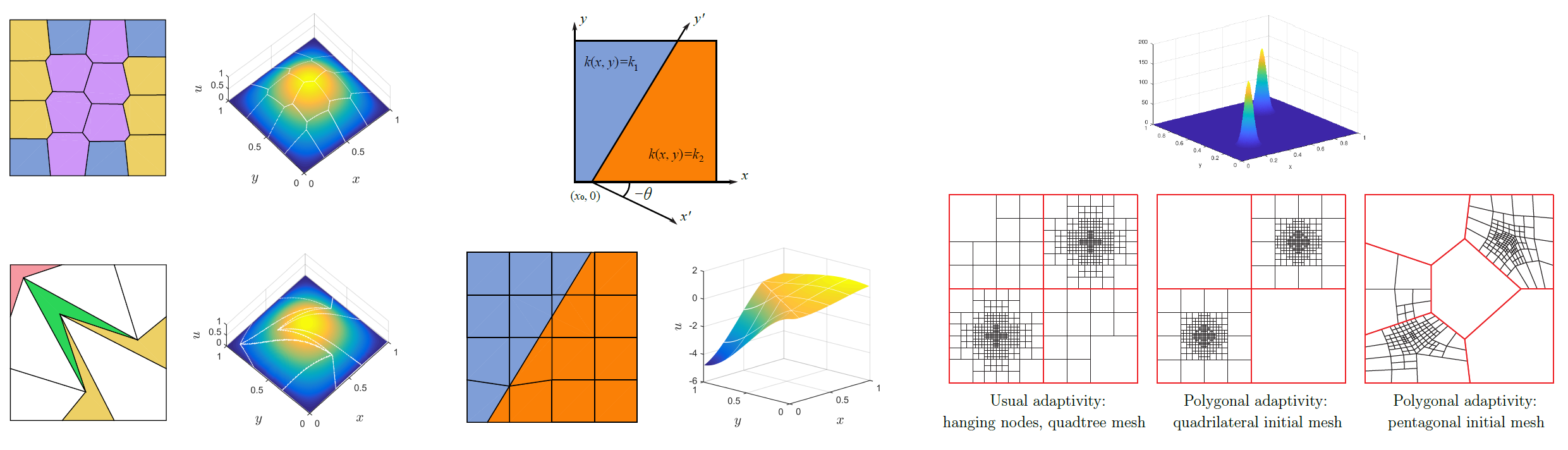
As another outgrowth of DPG methods, we developed high-order polygonal DPG (PolyDPG) methods by taking advantage of the properties of ultraweak formulations. These methods are compatible with arbitrary polygonal elements, distortion-tolerant, numerically stable without the need of extra stabilization terms (unlike other methods), and carry a natural a posteriori error estimator for adaptivity. They are useful in an array of applications ranging from topology optimization to crack propagation and geophysics. The code is available at www.polydpg.com.

Hydrodynamic stability

I am interested in the global stability properties of classical flows, like plane Couette flow, which are known to have infinite linear stability limit. The method of choice is the energy method, which is over a century old, and no significant improvements have ocurred since then. It uses the energy as a Lyapunov functional. By using new techniques from optimization, we try to find new Lyapunov functionals by posing the fluid system as an uncertain dynamical system that can be rewritten as a semidefinite program (SDP) with sum-of-squares (SOS) constraints.

Surpassing the energy method

By analyzing an idealized rotating flow we used these new optimization methods to prove the global stability of the flow for Reynolds numbers above the energy stability limit, thus finding a new lower bound for the global stability limit.

2D plane Couette flow

We analyzed 2D plane Couette flow, a very classical flow, whose only known lower bound for the global stability limit is the energy stability limit, established by Orr in 1907. We attempted to improve on the energy stability limit for a range of domain lengths, and the results show a clear improvement over the longstanding result.

Using an SDP to find Lyapunov functionals that prove global stability, the energy method was outperformed on an idealized rotating flow problem (left). Results show that the same techniques applied to 2D plane Couette flow yield the first improvement in over 110 years (middle and right).

Sparse polynomial optimization and finite element methods

By taking advantage of the sparsity of finite element discretizations, it is possible to apply recent results in sparse polynomial optimization to design practical algorithms that produce approximations (solved as SDPs) which rigorously converge to the global optimizers of nonlinear integral functionals of scientific interest.

Convergence to the global minimum of a quartic double-well problem in an ellipse (left). For the Swift-Hohenberg potential, among many local minimizers (middle), convergence to the global minimum is ensured (right).